Первые две не изображены, поскольку вэтом нет необходимости. Мы задаём уже готовую силу сопротивления. Третьей пренебрегаем, поскольку скорость движения не задана и может быть сколь угодно малой.Где вес самолёта, реакция опоры и сила лобового сопротивления?
Впрочем, даже в таком урезанном виде, эскиз свою функцию выполнил, поскольку мы с коллегой Borneo наконец-то пришли к согласию.
Именно так. Уточню только, что в приведенном мной выше выражении М = (F1 + F2) *H/2 указаны обе силы лишь для того, чтобы продемонстрировать действие именно ПАРЫ СИЛ. Поскольку они по величине равны, выражение может быть представлено и как М=F1*H, и как М=F2*H.Момент будет равен М=Ф1*Н. где Ф1 - сила, Н - плечо (расстояние до центра вращения самолета на земле)



 Ответить с цитированием
Ответить с цитированием

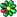

 , впрочем Мирный тоже прав, только, кроме реакций опор есть еще распределенная сила сопротивления и подъемная. Момент можно считать от носительно любой точки, второй закон Ньютона для вращения, от этого не зависит.
, впрочем Мирный тоже прав, только, кроме реакций опор есть еще распределенная сила сопротивления и подъемная. Момент можно считать от носительно любой точки, второй закон Ньютона для вращения, от этого не зависит.

